Trigonometri
I denne artikel skal vi gå i dybden med Trigonometri og dens indflydelse på vores samfund. Trigonometri er et emne, der har skabt stor interesse i de senere år, og det har sat gang i intense debatter og refleksioner på forskellige områder. Gennem historien har Trigonometri været en afgørende faktor i menneskers liv, og har påvirket den måde, de tænker, handler og forholder sig til deres miljø. I denne forstand er det afgørende at forstå vigtigheden af Trigonometri i dag, såvel som de implikationer, det har på vores daglige liv. Gennem denne artikel sigter vi på at belyse dette emne og analysere dets forskellige facetter, for at bidrage til en bedre forståelse og tilgang til Trigonometri i den aktuelle kontekst.
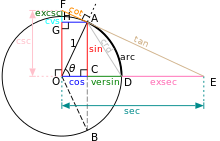
Trigonometri (fra græsk trigōnon = tre vinkler og metro = måle) er en gren af matematikken der behandler relationen mellem sider og vinkler i trekanter. Hertil er bl.a. knyttet disse fire trigonometriske funktioner:
Tilføjelser gælder for den retvinklede trekant.
- sinus (forkortet sin) = den modstående katete divideret med hypotenusen.[1]
- cosinus (forkort. cos) = den hosliggende katete divideret med hypotenusen.[1]
- tangens (forkort. tan eller tg) tangens er opkaldt efter tangent til enhedscirklen. tan = den modstående katete divideret med den hosliggende katete.[1]
- cotangens (forkortet cot) er defineret som reciprok tangens.[2]
De to funktioner, sinus og cosinus, er defineret ud fra enhedscirklen.[3] Hvorimod tangens og cotangens er defineret ud fra sinus og cosinus.[2]
Trekantberegninger
En trekant har tre sider og tre vinkler, dvs. der hører i alt seks værdier til en given trekant. Hvis tre af disse seks er givet (mindst én af dem en side), kan man ved hjælp af regneregler beregne de tre manglende værdier. De tre regler er:
- at summen af vinklerne i enhver trekant er 180°.[4]
- cosinusrelationerne[5] kaldes også den udvidede Pythagoras pga. lighed med Pythagoras' læresætning.
- sinusrelationenerne[6]
Regneopgaver af denne art kaldes for trekanttilfælde, og de inddeles efter hvilke oplysninger, der er givet.
Se også
- Grundrelationen - også kaldet idiotformlen
- Radian
- Vinkelfrekvens
- Sfærisk trigonometri – trigonometri udført på en kugles overflade i stedet for på en plan
Bøger
- Carstensen, Jens & Frandsen, Jesper (1990): Obligatorisk matematik. Forlaget Systime, Herning. ISBN 87-7783-630-8
- Holth, Klaus m.fl. (1987): Matematik Grundbog 1. Forlaget Trip, Vejle. ISBN 87-88049-18-3
Referencer
Eksterne henvisninger
- Trigonometriske funktioner Arkiveret 20. december 2005 hos Wayback Machine
Websites hjælper med trekantsberegning